Breaking Down Complexity: How Mechanistic Interpretability Actually Works
Learning the intuitions and motivations behind Mechanistic Interpretability.
Introduction
With state-of-the-art AI capable of beating PhDs in all scientific domains, ranking in the top 200 in competitive programming in the world and achieving a silver medal in the International Mathematical Olympiad, there’s an urgent need to understand their internal decision-making processes. Mechanistic interpretability has emerged as a promising approach to address this opacity by attempting to reverse engineer the computational processes occurring within neural networks.

This article aims to synthesise the fundamentals of current mechanistic interpretability advances, with a focus on three concepts that together offer us the most promising insight into these models we’ve had yet:
The circuits framework for understanding feature composition
Toy miniature models explaining the emergence of superposition
Sparse autoencoders (SAEs) as a practical tool for extracting interpretable features
This approach of dissecting these models provides promise of the ability to align AI towards human values or just away from potential harm in the future. Instead of having to associate AI systems with black boxes, only evaluable from the outside, we can begin to understand and modify the internal mechanisms that produce their behaviour. This is a key differentiator to other safety approaches like RLHF which focus on steering model outputs from an external point of view.
These recent advancements, I argue, present an important inflection point in mechanistic interpretability, where we can reliably move from theoretical possibility to a practical tool for controlling very capable AI.
This is exemplified through the first emerging mechanistic interpretability products, where generalised implementations of interpretability are available as a paid service, like Ember from Goodfire:

Through this article, I hope to address specific themes of:
Show why mechanistic interpretability matters through concrete examples
Explain the fundamental challenges that make it complicated and difficult
Introduce the key tools researchers use to solve these challenges
Demonstrate how these tools combine to enable understanding and possible further control of AI systems
The Core Challenge: Why Neural Networks are Hard to Understand
Neural networks achieve remarkable performance through distributed representations that are fundamentally different from human-interpretable concepts. Understanding these representations requires grappling with three interrelated challenges: the dimensionality problem, superposition, and polysemanticity.
To understand why modern interpretability techniques matter, we must first understand the fundamental challenge they're trying to solve: neural networks don't store information the way we expect or hope. Explained explicitly:
Networks have a select number of neurons (in the billions), but are capable of representing many more concepts (or features)
Traditional assumption: one neuron = one concept
Reality: neurons represent multiple concepts simultaneously
Dimensionality and Compression
Current transformer-based LLMs need to learn billions of concepts, often defined as features. These features may be facts about New York City, how logarithms work, or where Pizza originated from.
By default, it’d make intuitive sense for models to dedicate specific neurons to specific features, so they activate specifically in response to a user's question “Where does Pizza originate from?”
However, this quickly becomes intractable as there are vastly more features than neurons in each layer of a model.
Superposition
An emergent property of large-scale models inherently handles this problem of dimensionality elegantly. Specifically, they compress information by overlapping multiple features across different neurons, this is known as superposition.

This geometric representation of concepts allows for networks to effectively store a larger amount of features than individual neurons. This works in practice because many concepts existing in the world are naturally sparse.
Sparsity in this sense means that they occur rarely and seldom need to be processed simultaneously. For example, the birthplace of an individual celebrity may come up in less than one in a billion training tokens, yet modern LLMs will learn this fact (and an extraordinary amount of other facts) about the world.
Polysemanticity
While superposition elegantly solves the compression problem, this entanglement of features creates challenges for interpretability. When individual neurons participate in representing multiple concepts - a phenomenon known as polysemanticity - we cannot reliably isolate and study individual features through simple methods.

Polysemanticity isn't caused by the network finding semantic relationships between concepts or features, instead, it’s a direct consequence of superposition. When networks need to represent more features than they have neurons, they mathematically optimise to share neural space by arranging features in high-dimensional geometric patterns. This leads to individual neurons participating in representing multiple unrelated concepts.
This is demonstrated in the Toy Models work by Anthropic (which we’ll dig into shortly), where researchers showed that:
This behaviour emerges even with randomly generated, explicitly unrelated features, indicating that feature importance isn't solely dependent on semantic meaning
The geometric arrangements are determined by sparsity and feature importance. A key concept where some features are statistically more significant in influencing the model's predictions than others. Feature importance quantifies how much each input feature contributes to the model's overall output, with more important features having a more substantial impact on the model's decision-making process
The same patterns occur predictably across different models and tasks, demonstrating what's known as universality in mechanistic interpretability, suggesting that feature importance plays a consistent role in how neural networks organise and process information across model architectures and size
This mixed representation presents challenges for AI safety and alignment:
Feature Isolation: It becomes difficult to identify and modify specific capabilities when they are entangled across many neurons. For example, attempting to adjust a model's mathematical abilities might unintentionally affect its language processing if these features share neural pathways.
Unintended Effects: Modifying neurons to affect one concept may have unexpected effects on other concepts that share those neurons. A change intended to reduce aggressive language might accidentally impact polite but firm communication.
Safety Analysis: Potentially harmful capabilities could be subtly encoded across many neurons, making them difficult to detect and control. Researchers have found features related to:
Security vulnerabilities and code backdoors
Bias (from overt slurs to subtle prejudices)
Deceptive and power-seeking behaviors
Sycophancy (telling users what they want to hear)
Dangerous content (like instructions for conducting harmful and illegal activity)
Three Complementary Approaches To Mechanistic Interpretability
The breakthrough in modern mechanistic interpretability comes from combining three complementary approaches that together allow us to understand and manipulate neural networks' internal representations. Each approach addresses a different aspect of the interpretability challenge:
Circuits: Understanding Feature Composition
Toy Models: Formalising Superposition
Sparse Autoencoders: Extracting Interpretable Features
Circuits: Understanding Feature Combinations
The "circuits" framework, developed in early interpretability work, provides a way to understand how neural networks combine simple features into more complex ones. Just as electronic circuits combine basic components into complex devices, neural circuits show how networks build sophisticated capabilities from simpler pieces.
Now that we understand how neural networks store information through superposition, we can look into the question of how networks combine these superposed features to perform actual computation? The circuits framework, developed by OpenAI researchers in 2020, provides examples and claims to understand how these work.
Despite the complexity of superposition, neural networks combine features in surprisingly systematic and interpretable ways. Consider how a simple vision model might detect a car:
Features
Windows (4b:237) excites the car detector at the top
Car Body (4b:491) provides strong excitation, especially at the bottom
Wheels (4b:373) contribute additional bottom excitation
Weight and position these features appropriately
Apply non-linear operations to filter out non-matching patterns
The circuits paper introduced tests to verify the occurrence of circuits in neural networks. This provided a framework for identifying and understanding how sparse features combine to form more complex concepts in circuits. Having this understanding provides us with the opportunity to look inside the model.
Toy Models: Formalising the Mathematics of Superposition
Toy Models help us crucially understand why neural networks use superposition. Researchers found that through studying very simple neural networks, superposition is a mathematically optimal behaviour that naturally emerges when networks need to store more features than they have neurons in a layer.
Imagine trying to store 100 different facts in a network with only 30 neurons. The toy model experiments explore exactly this scenario:
Features: Simple patterns the network needs to learn (like our 100 facts)
Limited Space: Fewer neurons than features (like our 30 neurons)
Sparsity: Most features are rarely used together (referred to above as natural sparsity, how we rarely need to recall all 100 facts at once)
Through this natural sparity, the network learns to “overlap” features across multiple neurons in specific geometric ways such as through the 2D plane example earlier.
The toy model experiments revealed several fascinating patterns:
Phase Changes: When features are dense (frequently used together), networks behave conventionally - each neuron handles one feature, and less important features are simply ignored. But as features become sparser, the network begins using superposition to store more information.
Geometric Organisation: Features arrange themselves into regular geometric patterns that maximise how much information can be stored
Importance-Based Structure: Networks balance feature importance against interference. Critical features get more "dedicated" neural space, while less important features share space through superposition. This explains why some neurons in real networks appear monosemantic while others are polysemantic.
For example, in an animal detector model, a commonly used feature such as “cat faces” detection may get its own neural space. Whereas, less important features such as "cat whiskers" and "cat stripes" may share a neuron for two reasons:
These features are less critical than faces for identification
They rarely need to be detected simultaneously (a cat usually doesn't show both prominent whiskers and prominent stripes in the same image area)
Why This Matters
These findings from toy models help us understand real neural networks in several ways:
They explain why polysemantic neurons form and under what conditions we should expect to find them
They suggest what geometric patterns we should look for when trying to extract features
They help us predict how different architectural choices might affect feature organisation
This research crucially laid the foundation of predictability in neural network observations, explicitly outlining how large-scale neural networks store and utilise knowledge in limited space.
Sparse Autoencoders: Unpacking Compressed Features
With our understanding of how and why networks use superposition, we can now tackle a crucial question: how do we reliably extract and manipulate these overlapping features? This is where Sparse Autoencoders (SAEs) come into play.
SAEs represent a way to interpret these compressed representations. They act as a "translation layer" that unpacks the compressed, overlapping features into a larger, more interpretable space. The key mechanisms are:
Map the network's activations to a larger space (more neurons than the original)
Use sparsity constraints to ensure each input only activates a few neurons
Naturally encourage each neuron to specialise in one specific concept
In practice, this looks like:
Input: Original network activations (n dimensions)
Encoder: Maps to larger space (m dimensions, m > n)
Hidden Layer: Sparse representation of features
Decoder: Maps back to original space
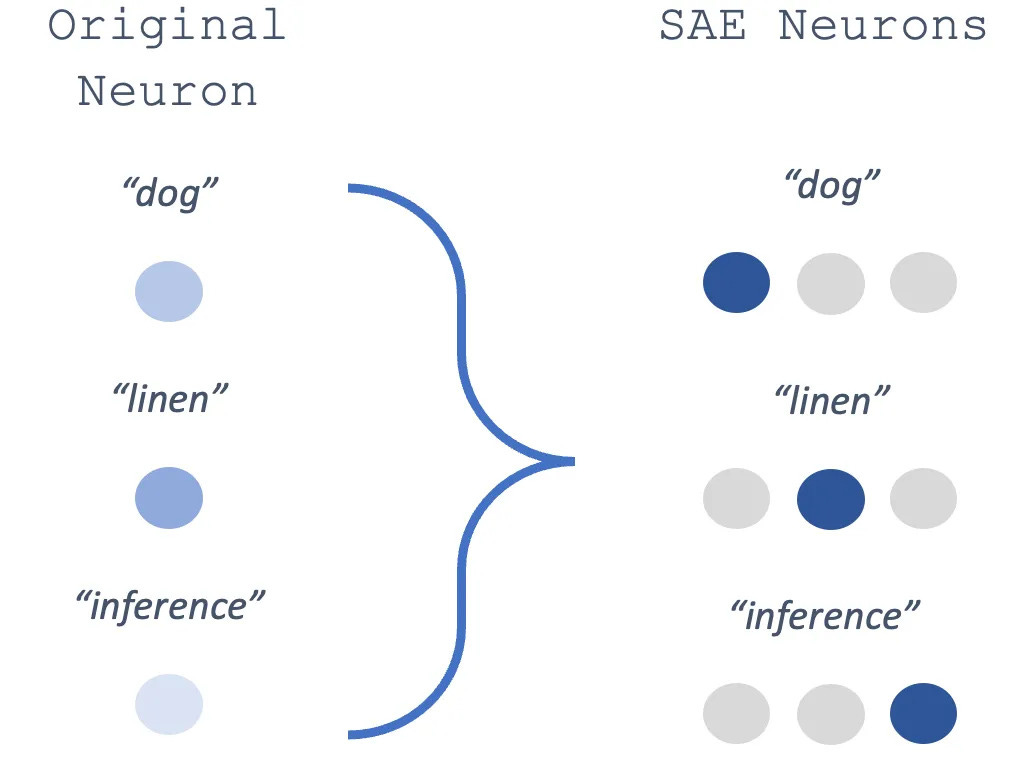
Where the end result can be simplified as this:
Schematic of a sparse-autoencoder (SAE) in action. A single neuron in the original LLM responds to multiple words (“dog”, “linen”, “inference”). A mapping is learned to the SAE space, in which these activations can be uncorrelated. Source
This creates a clear interpretable representation of features through monosemanticity, the opposite of polysemanitcity.
Each SAE neuron specialises in a single feature because:
There's enough room for features to have their own neurons
Sparsity discourages neurons from handling multiple features
Reconstruction ensures we capture all important information
This creates great opportunities for safety by allowing for the identification of specifically dangerous, deceptive or misaligned behavioural features. These can then be “steered” in positive or negative directions to amend the models' output, as we saw previously.
Through the more recent scaling of SAEs and the conversion to monosemanticity, we can observe more complicated features being extracted and interpretable.
From the Anthropic paper, here a prompt is sent with bug-free code with the clamped “code error” feature to a large positive activation. We see that the model proceeds to hallucinate an error message:
Understanding Anthropic's Research: Putting It All Together
These three approaches - Circuits, toy models and SAEs, combine nicely into a concrete way to identify, evaluate and manipulate large-scale LLMs such as Claude 3.
The process:
Feature Detection (Using SAEs)
Initial observation: A feature that activates for "Golden Gate Bridge"
Expanded space reveals it's genuinely monosemantic
Activation patterns show reliable, specific responses to the bridge
Understanding Implementation (Using Circuits Framework)
Feature combines:
Colour detection ("golden" and "red")
Bridge structure recognition
San Francisco context
Architectural style markers
Geometric Analysis (Using Toy Models Understanding)
Feature sits in a regular geometric arrangement with:
Other landmark features
Bridge-related features
San Francisco features
This framework can be utilised through direct manipulation of this identified feature. If we were to artificially boost the activation of “Golden Gate Bridge” in Claude 3, we’d see:
Primary effects (from circuits):
More references to the bridge
Bridge-related descriptions
San Francisco context
Side effects (from geometric analysis):
Minimal impact on other landmark features
Some boost to bridge-related concepts
Slight influence on SF features
“First, we study a Golden Gate Bridge feature (34M/31164353). Its greatest activations are essentially all references to the bridge, and weaker activations also include related tourist attractions, similar bridges, and other monuments.”
Each approach strengthens the others:
SAEs reveal what features exist
Circuits show how they're implemented
Toy Models explain why they're organised this way
This creates a scalable, working model of how we can approach analysing the intrinsic decision-making of neural networks.
How Feature Steering is already a sign of encouragement
More recently, Anthropic has published promising advancements in our ability to directly influence model behaviour using the techniques we’ve discussed so far. By leveraging an understanding of circuits, superposition and monosemantic features, SAEs have been successful in adjusting specific activations of features while maintaining benchmark performance on the MMLU.
Additionally, finding high-level features such as “Neutrality” and “Multiple Perspectives” and steering them positively, results in dramatic decreases in bias model output across many domains.
“Our results suggest that feature steering may be an effective way to mitigate some forms of social biases without significantly impacting model capabilities. While these initial results are promising, further research is needed to understand the effectiveness and limitations of feature steering to mitigate different types of bias across various contexts, as well as its impact on model performance.”
Conclusion
This article has aimed to provide an intuitive understanding of the core concepts behind the recent advancements in mechanistic interpretability. By breaking down the fundamental challenges of dimensionality, superposition, and polysemanticity, we can better appreciate why neural networks organise information in seemingly counterintuitive ways.
The three approaches we've explored of circuits, toy models, and sparse autoencoders each address different aspects of this challenge, collectively offering a framework for effectively looking inside and amending these "black boxes".
For readers interested in diving deeper into the technical details, this conceptual foundation should provide helpful context for engaging with the primary literature, particularly:
The original Circuits paper from OpenAI, establishes the framework for understanding feature composition - Zoom In: An Introduction to Circuits
Anthropic's Toy Models of Superposition, which provides a mathematical formalisation of feature organisation - Toy Models of Superposition
The recent work on sparse autoencoders and monosemanticity, which demonstrates these principles at scale - Towards Monosemanticity: Decomposing Language Models With Dictionary Learning and Scaling Monosemanticity: Extracting Interpretable Features from Claude 3 Sonnet
Finally, the more recent feature steering for bias mitigation by Anthropic - Evaluating feature steering: A case study in mitigating social biases \ Anthropic
Failed to render LaTeX expression — no expression found